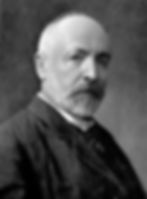Click the tartan to view its entry in The Scottish Registers of Tartans which includes registration details, restrictions, and registrant information.
Unregistered tartans may link to one of the web's online design environments for similar information.
For any questions about reproduction of designs or weaving of these tartans, please contact the registrant directly or via this website.
Math 2.0 Day
"No one shall expel us from the paradise that Cantor has created."
~ David Hilbert (1862-1943)
Mathematicians take note! Math 2.0 Day celebrates the importance of the relationship between math and technology. Special mathematical relationships sometimes form distinctive and suggestive patterns, such as the Cantor Tartan, a visual representation derived from pure mathematics! German mathematician Georg Cantor played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor's contributions include Cantor's paradox, Cantor's theorem, one-to-one correspondence, and transfinite numbers. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers, which implied the existence of an infinity of infinities! This concept was of great philosophical interest which caused controversy in both the mathematical world and attracted negative attention from some Christian theologians who saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God! Mathematicians interested in weird sets may be familiar with the Cantor set (a derived set of points on a line segment with interesting topological properties). Extrapolations of this set form interesting patterns, including Cantor Dust, Cantor Cubes, and the Cantor Tartan! You can create a cantor tartan by starting from a unit square and erasing the central third strip from rectangles, recursively. Then rotate a duplicate on top by 90 degrees. The Cantor Tartan has the interesting property such that any rectangle with dimensions smaller than one can be covered by the Cantor Tartan. There is even a Fractal Calculus of Functions on Cantor Tartan Spaces! ♾️ 📐📏 ⚗️⚛️
Georg Cantor (1845-1918) was a renowned German mathematician known for his groundbreaking work in set theory and the development of the concept of infinity. Born on March 3, 1845, in Saint Petersburg, Russia, Cantor displayed exceptional mathematical talent from an early age.
After completing his secondary education in Germany, Cantor went on to study mathematics and physics at the University of Berlin. He was deeply influenced by his mentors, Leopold Kronecker and Karl Weierstrass, who encouraged his exploration of mathematical concepts.
Cantor's most significant contributions lie in the field of set theory. In 1874, he published a seminal paper introducing the concept of "transfinite" numbers, which demonstrated the existence of different sizes of infinity. This groundbreaking notion challenged conventional mathematical thought and led to the development of a new branch of mathematics known as "infinity mathematics" or "transfinite set theory."
One of Cantor's most influential achievements was his establishment of a rigorous foundation for set theory through the introduction of the concept of "cardinality." He developed a framework to compare the sizes of infinite sets using one-to-one correspondences and introduced the concept of the "power set," which showed that there are different degrees of infinity.
Despite his profound contributions, Cantor's work was met with resistance and criticism from some mathematicians of his time. The concept of infinity and the idea of different sizes of infinity were viewed as unconventional and paradoxical by many. Cantor faced personal and professional challenges due to the backlash and struggled with mental health issues throughout his life.
Nevertheless, Cantor continued his groundbreaking work and published numerous papers and books on set theory. His legacy as the founder of modern set theory and the pioneer of the study of infinity remains unchallenged.
Georg Cantor passed away on January 6, 1918, in Halle, Germany, leaving behind a rich mathematical legacy that continues to influence mathematicians and philosophers to this day. His work has had a profound impact on our understanding of the nature of infinity and the foundations of mathematics. Cantor's perseverance and intellectual courage have solidified his place among the greatest mathematicians of all time.
To see an animation of the creation of the Cantor tartan, click Georg Cantor's photograph.